g0501_0600.s0563_binary_tree_tilt.readme.md Maven / Gradle / Ivy
Go to download
Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-kotlin Show documentation
Show all versions of leetcode-in-kotlin Show documentation
Kotlin-based LeetCode algorithm problem solutions, regularly updated
563\. Binary Tree Tilt
Easy
Given the `root` of a binary tree, return _the sum of every tree node's **tilt**._
The **tilt** of a tree node is the **absolute difference** between the sum of all left subtree node **values** and all right subtree node **values**. If a node does not have a left child, then the sum of the left subtree node **values** is treated as `0`. The rule is similar if the node does not have a right child.
**Example 1:**
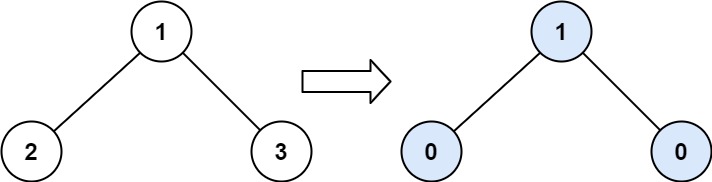
**Input:** root = [1,2,3]
**Output:** 1
**Explanation:**
Tilt of node 2 : |0-0| = 0 (no children)
Tilt of node 3 : |0-0| = 0 (no children)
Tilt of node 1 : |2-3| = 1 (left subtree is just left child, so sum is 2; right subtree is just right child, so sum is 3)
Sum of every tilt : 0 + 0 + 1 = 1
**Example 2:**
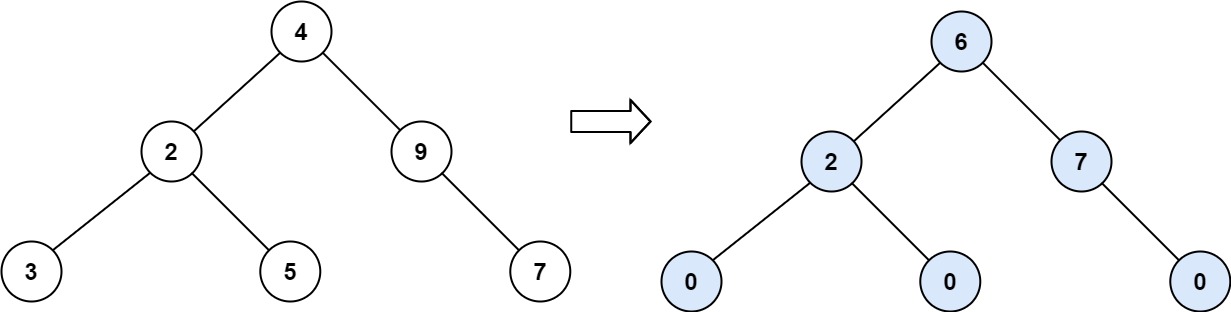
**Input:** root = [4,2,9,3,5,null,7]
**Output:** 15
**Explanation:**
Tilt of node 3 : |0-0| = 0 (no children)
Tilt of node 5 : |0-0| = 0 (no children)
Tilt of node 7 : |0-0| = 0 (no children)
Tilt of node 2 : |3-5| = 2 (left subtree is just left child, so sum is 3; right subtree is just right child, so sum is 5)
Tilt of node 9 : |0-7| = 7 (no left child, so sum is 0; right subtree is just right child, so sum is 7)
Tilt of node 4 : |(3+5+2)-(9+7)| = |10-16| = 6 (left subtree values are 3, 5, and 2, which sums to 10; right subtree values are 9 and 7, which sums to 16)
Sum of every tilt : 0 + 0 + 0 + 2 + 7 + 6 = 15
**Example 3:**
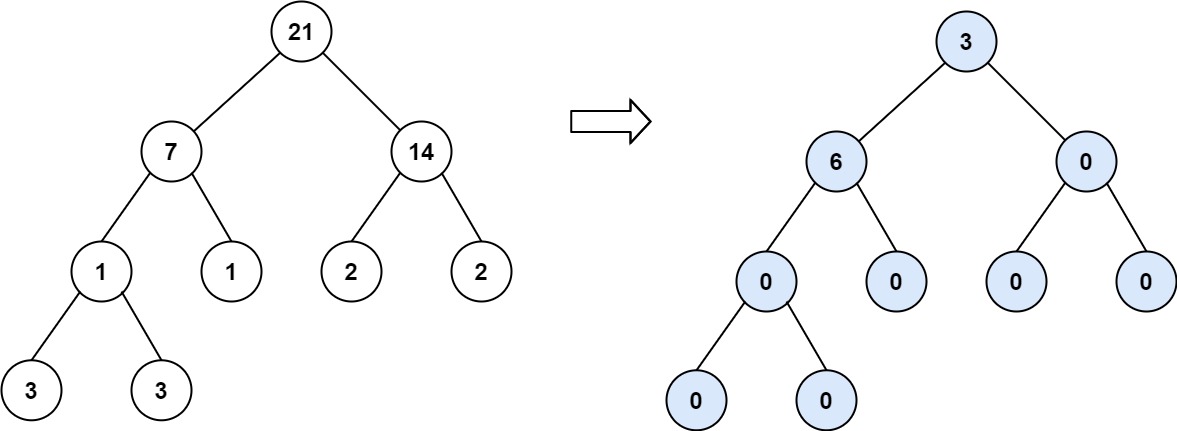
**Input:** root = [21,7,14,1,1,2,2,3,3]
**Output:** 9
**Constraints:**
* The number of nodes in the tree is in the range [0, 104].
* `-1000 <= Node.val <= 1000`