• Home
• com.github.javadev
• leetcode-in-kotlin
• 1.20
• source code
• readme.md

×

Project download

Many resources are needed to download a project. Please understand that we have to compensate our server costs. Thank you in advance.
Project price only 1 $

You can buy this project and download/modify it how often you want.

g0701_0800.s0749_contain_virus.readme.md Maven / Gradle / Ivy

749\. Contain Virus

Hard

A virus is spreading rapidly, and your task is to quarantine the infected area by installing walls.

The world is modeled as an `m x n` binary grid `isInfected`, where `isInfected[i][j] == 0` represents uninfected cells, and `isInfected[i][j] == 1` represents cells contaminated with the virus. A wall (and only one wall) can be installed between any two **4-directionally** adjacent cells, on the shared boundary.

Every night, the virus spreads to all neighboring cells in all four directions unless blocked by a wall. Resources are limited. Each day, you can install walls around only one region (i.e., the affected area (continuous block of infected cells) that threatens the most uninfected cells the following night). There **will never be a tie**.

Return _the number of walls used to quarantine all the infected regions_. If the world will become fully infected, return the number of walls used.

**Example 1:**

![](https://assets.leetcode.com/uploads/2021/06/01/virus11-grid.jpg)

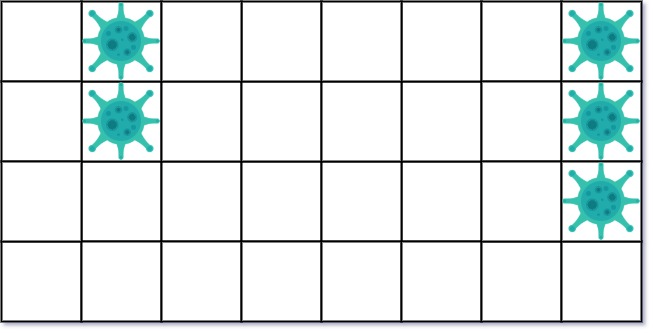
**Input:** isInfected = [[0,1,0,0,0,0,0,1],[0,1,0,0,0,0,0,1],[0,0,0,0,0,0,0,1],[0,0,0,0,0,0,0,0]]

**Output:** 10

**Explanation:** There are 2 contaminated regions. On the first day, add 5 walls to quarantine the viral region on the left. The board after the virus spreads is: 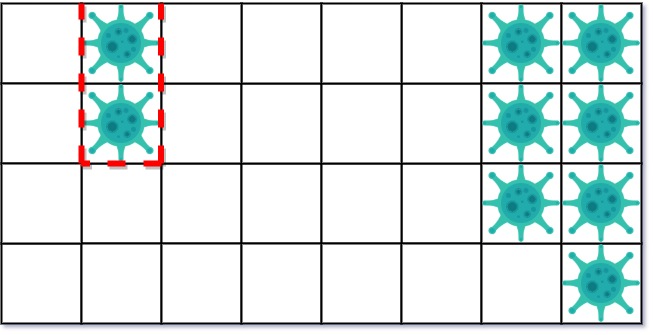![](https://assets.leetcode.com/uploads/2021/06/01/virus12edited-grid.jpg) On the second day, add 5 walls to quarantine the viral region on the right. The virus is fully contained. 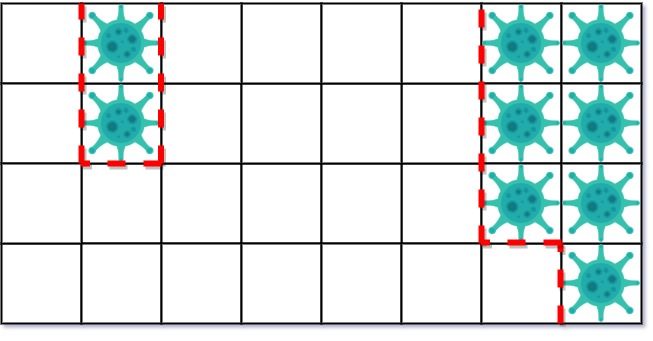![](https://assets.leetcode.com/uploads/2021/06/01/virus13edited-grid.jpg)

**Example 2:**

![](https://assets.leetcode.com/uploads/2021/06/01/virus2-grid.jpg)

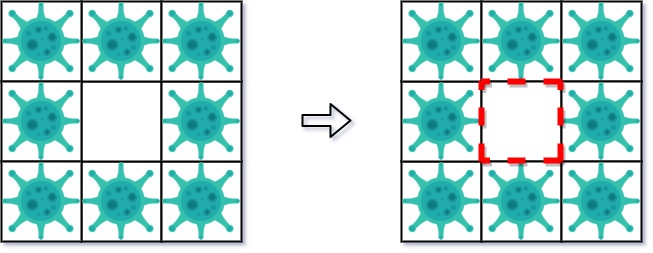
**Input:** isInfected = [[1,1,1],[1,0,1],[1,1,1]]

**Output:** 4

**Explanation:** Even though there is only one cell saved, there are 4 walls built. Notice that walls are only built on the shared boundary of two different cells.

**Example 3:**

**Input:** isInfected = [[1,1,1,0,0,0,0,0,0],[1,0,1,0,1,1,1,1,1],[1,1,1,0,0,0,0,0,0]]

**Output:** 13

**Explanation:** The region on the left only builds two new walls.

**Constraints:**

*   `m == isInfected.length`
*   `n == isInfected[i].length`
*   `1 <= m, n <= 50`
*   `isInfected[i][j]` is either `0` or `1`.
*   There is always a contiguous viral region throughout the described process that will **infect strictly more uncontaminated squares** in the next round.