• Home
• com.github.javadev
• leetcode-in-kotlin
• 1.20
• source code
• readme.md

×

Project download

Many resources are needed to download a project. Please understand that we have to compensate our server costs. Thank you in advance.
Project price only 1 $

You can buy this project and download/modify it how often you want.

g0701_0800.s0787_cheapest_flights_within_k_stops.readme.md Maven / Gradle / Ivy

787\. Cheapest Flights Within K Stops

Medium

There are `n` cities connected by some number of flights. You are given an array `flights` where flights[i] = [fromi, toi, pricei] indicates that there is a flight from city fromi to city toi with cost pricei.

You are also given three integers `src`, `dst`, and `k`, return _**the cheapest price** from_ `src` _to_ `dst` _with at most_ `k` _stops._ If there is no such route, return `-1`.

**Example 1:**

![](https://assets.leetcode.com/uploads/2022/03/18/cheapest-flights-within-k-stops-3drawio.png)

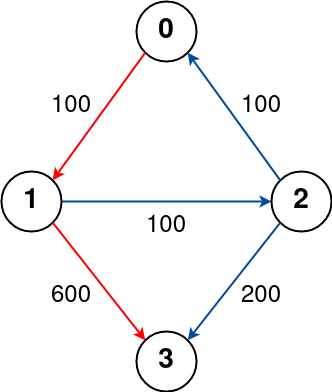
**Input:** n = 4, flights = [[0,1,100],[1,2,100],[2,0,100],[1,3,600],[2,3,200]], src = 0, dst = 3, k = 1

**Output:** 700

**Explanation:** 

The graph is shown above. 

The optimal path with at most 1 stop from city 0 to 3 is marked in red and has cost 100 + 600 = 700. 

Note that the path through cities [0,1,2,3] is cheaper but is invalid because it uses 2 stops.

**Example 2:**

![](https://assets.leetcode.com/uploads/2022/03/18/cheapest-flights-within-k-stops-1drawio.png)

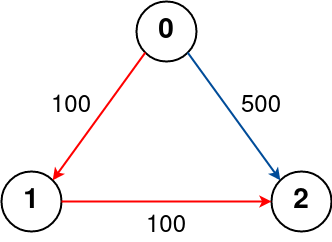
**Input:** n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 1

**Output:** 200

**Explanation:** 

The graph is shown above. 

The optimal path with at most 1 stop from city 0 to 2 is marked in red and has cost 100 + 100 = 200.

**Example 3:**

![](https://assets.leetcode.com/uploads/2022/03/18/cheapest-flights-within-k-stops-2drawio.png)

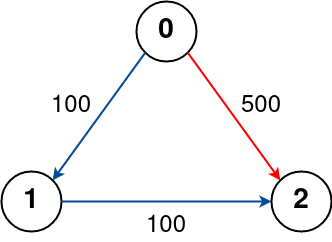
**Input:** n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 0

**Output:** 500

**Explanation:** 

The graph is shown above. 

The optimal path with no stops from city 0 to 2 is marked in red and has cost 500.

**Constraints:**

*   `1 <= n <= 100`
*   `0 <= flights.length <= (n * (n - 1) / 2)`
*   `flights[i].length == 3`
*   0 <= fromi, toi < n
*   fromi != toi
*   1 <= pricei <= 104
*   There will not be any multiple flights between two cities.
*   `0 <= src, dst, k < n`
*   `src != dst`