g2401_2500.s2463_minimum_total_distance_traveled.readme.md Maven / Gradle / Ivy
Go to download
Show more of this group Show more artifacts with this name
Show all versions of leetcode-in-kotlin Show documentation
Show all versions of leetcode-in-kotlin Show documentation
Kotlin-based LeetCode algorithm problem solutions, regularly updated
2463\. Minimum Total Distance Traveled
Hard
There are some robots and factories on the X-axis. You are given an integer array `robot` where `robot[i]` is the position of the ith robot. You are also given a 2D integer array `factory` where factory[j] = [positionj, limitj] indicates that positionj is the position of the jth factory and that the jth factory can repair at most limitj robots.
The positions of each robot are **unique**. The positions of each factory are also **unique**. Note that a robot can be **in the same position** as a factory initially.
All the robots are initially broken; they keep moving in one direction. The direction could be the negative or the positive direction of the X-axis. When a robot reaches a factory that did not reach its limit, the factory repairs the robot, and it stops moving.
**At any moment**, you can set the initial direction of moving for **some** robot. Your target is to minimize the total distance traveled by all the robots.
Return _the minimum total distance traveled by all the robots_. The test cases are generated such that all the robots can be repaired.
**Note that**
* All robots move at the same speed.
* If two robots move in the same direction, they will never collide.
* If two robots move in opposite directions and they meet at some point, they do not collide. They cross each other.
* If a robot passes by a factory that reached its limits, it crosses it as if it does not exist.
* If the robot moved from a position `x` to a position `y`, the distance it moved is `|y - x|`.
**Example 1:**
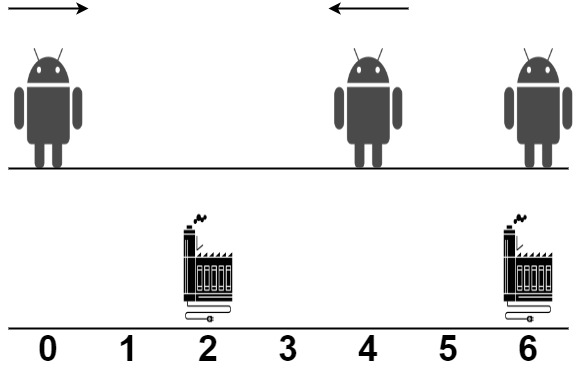
**Input:** robot = [0,4,6], factory = [[2,2],[6,2]]
**Output:** 4
**Explanation:** As shown in the figure:
- The first robot at position 0 moves in the positive direction. It will be repaired at the first factory.
- The second robot at position 4 moves in the negative direction. It will be repaired at the first factory.
- The third robot at position 6 will be repaired at the second factory. It does not need to move.
The limit of the first factory is 2, and it fixed 2 robots.
The limit of the second factory is 2, and it fixed 1 robot.
The total distance is |2 - 0| + |2 - 4| + |6 - 6| = 4. It can be shown that we cannot achieve a better total distance than 4.
**Example 2:**
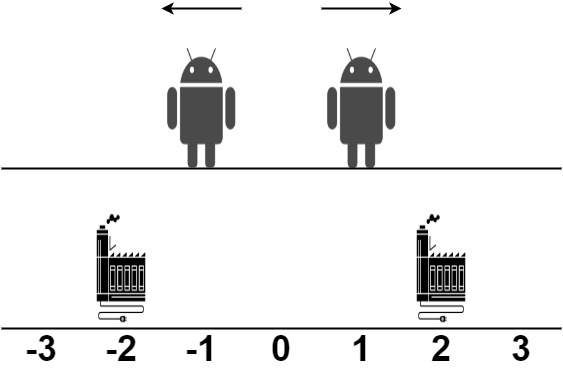
**Input:** robot = [1,-1], factory = [[-2,1],[2,1]]
**Output:** 2
**Explanation:** As shown in the figure:
- The first robot at position 1 moves in the positive direction. It will be repaired at the second factory.
- The second robot at position -1 moves in the negative direction. It will be repaired at the first factory.
The limit of the first factory is 1, and it fixed 1 robot. The limit of the second factory is 1, and it fixed 1 robot.
The total distance is |2 - 1| + |(-2) - (-1)| = 2. It can be shown that we cannot achieve a better total distance than 2.
**Constraints:**
* `1 <= robot.length, factory.length <= 100`
* `factory[j].length == 2`
* -109 <= robot[i], positionj <= 109
* 0 <= limitj <= robot.length
* The input will be generated such that it is always possible to repair every robot.